| Introdução |
O médico ao solicitar um exame de rastreamento, deve-se levar em conta os seguintes critérios: sensibilidade, especificidade, efetividade, custo e a carga de sofrimento que a condição médica pode ocasionar. Diante disso, um teste deve ter alta sensibilidade e especificidade, pois geralmente a prevalência das doenças rastreadas é baixa1 .
A sensibilidade de um teste é a proporção de pessoas portadoras de uma doença que têm o teste positivo, ou seja, a capacidade de detectar verdadeiros-positivos. Já a especificidade é a proporção dos não portadores de doença com exames negativos, ou seja, os verdadeiro-negativos.
Uma maneira de divulgar a performance de um exame dando uma informação semelhante à sensibilidade e à especificidade é o likelihood ratio ou razão de verossimilhança. Este indica quantas vezes o teste aumenta (likelihood ratio positiva) ou diminui (likelihood ratio negativa) a probabilidade pré-teste. Seu resultado é mais simples de ser aplicado na prática clínica, no qual o resultado maior que 1 indica aumento progressivo na chance da doença e menor que 1 indica diminuição progressiva na chance da doença1 .
| Likehood ratio |
O likelihood ratio (LR) é a probabilidade de um achado estar presente em um paciente com a doença investigada. É calculado a partir da proporção de pacientes com doença que apresentam um determinado achado dividido pela proporção de pacientes sem doença que também apresentam o mesmo achado.
.jpg)
Por exemplo, entre pacientes com distensão abdominal, a febre está presente em 80% dos pacientes com ascite confirmada e em 40% sem ascite. O LR para febre em ascite confirmada é de 2,0 (80% divididos por 40%).
LR pode variar de 0 até infinido. Achados com LRs maiores que 1 aumentam a probabilidade de o achado estar presente na doença; quanto maior o LR, mais convincente é o argumento a favor do achado na doença. Achados cujos LRs se situam entre zero e 1 diminuem a probabilidade do achado na doença; quanto mais próximo o LR estiver de zero, mais convincente será o achado não está associado à doença. Achados cujos LRs são iguais a 1 carecem de valor diagnóstico porque não mudam a probabilidade de forma alguma.
Como exemplo, temos o gráfico 1 que são resultados de um exame para teste de ferritinina sérica que testa anemia por deficiência de ferro. O LR de 51,8 para <15 mg/dL resulta em evidências muito fortes para determinar a anemia por deficiência de ferro. Por outro lado, LR 0,08 para >100 mg/dL mostra que não há associação2.
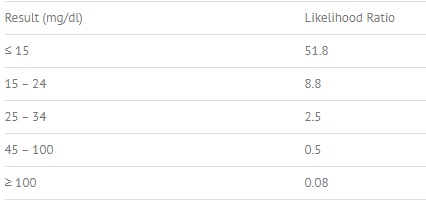
Gráfico 1: Resultados de um exame para teste de ferritinina sérica que testa anemia por deficiência de ferro.
| Como utilizar o LR para determinar a probabilidade |
- > Métodos convencionais
Probabilidade pré-teste (prevalência): é a probabilidade de o paciente possuir determinada doença antes de se aplicar um achado clínico ou um resultado de teste diagnóstico. Por exemplo, se 2 em 5 pacientes com distensão abdominal tem ascite, a probabilidade pré-teste é de 40%. O método tradicional de aplicar o achado, que seria a febre (LR= 2) é converter a probabilidade pré-teste(PPRE) para a pré-test odds (OPRE), usando OPRE= PPRE/(1 – PPRE), e após, multiplicar o OPRE pelo LR para achar o pós-teste odds OPOST = LR x OPRE e então, converter o pós-teste odds para probabilidade do pós-teste usando PPOST = OPOST/(1 + OPOST). No caso, achamos que a febre (LR =2.0) aumenta a probabilidade de ascite de 40% para 57% (OPRE = 0,4/(1 – 0,4)= 0.667; OPOST = 0.667 x 2,0 = 1,333; PPOST = 1,333/(1 + 1,333) = 0,57 ou 57%)3.
- Através de gráfico
O gráfico 2 é um gráfico fácil de usar como exemplo pois ilustra a relação entre a probabilidade pré-teste (eixo x) e a probabilidade pós-teste (eixo y), dado o LR do achado4. A linha reta que divide o gráfico em uma metade superior esquerda e metade inferior direita descreve o LR de 1, que não tem valor discriminatório. Os achados físicos que argumentam para a doença (ou seja, LRs> 1) aparecem na metade superior esquerda do gráfico; quanto maior o valor do LR, mais a curva se aproxima do canto superior esquerdo. Os achados físicos que argumentam contra a doença (ou seja, LRs <1) aparecem na metade inferior direita do gráfico: quanto mais próximo o LR está de zero, mais a curva se aproxima do canto inferior direito.
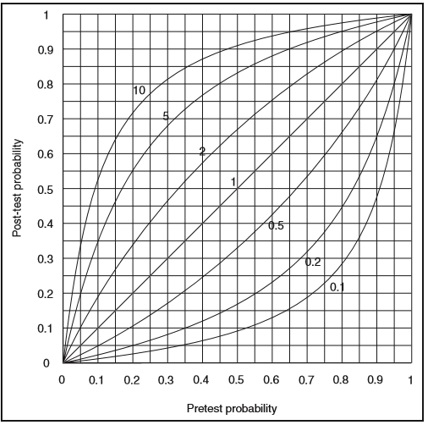
Gráfico 2: Probabilidade e likelihood ratios4.
Mas como o médico utiliza esse gráfico? O médico identifica no eixo x a probabilidade pré-teste do paciente e estende uma linha para cima até encontrar a curva LR para o achado físico. Então,o médico estende uma linha horizontal deste ponto ao eixo y para identificar a probabilidade pós-teste.
Em um caso hipotético, em pacientes com hipertensão pulmonar, a probabilidade pré-teste de regurgitação tricúspide é de 42% (0,42)4. A linha é desenhada para cima a partir de 0,42 no eixo X até encontrar a curva de LR. Quando encontra, outra linha é desenhada no eixo Y para demonstrar a probabilidade pós teste (88%) como listra o gráfico 3.
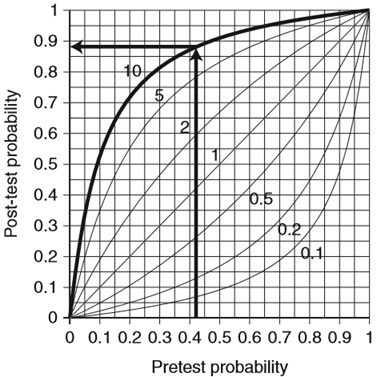
Gráfico 3: Probabilidade e likelihood ratios: pacientes com hipertensão pulmonar4.
Essas curvas ilustram um ponto importante: os achados são diagnosticamente mais úteis quando aplicados a pacientes que têm probabilidade pré-teste na faixa entre 20% a 80% pois divergem mais de LR = 1. Se a probabilidade do pré-teste é muito alta ou muito baixa, as curvas se agruparão perto da linha LR =1.
- Estatística
O clínico pode evitar o uso de gráficos e, em vez disso, aproximar a probabilidade pós-teste, lembrando-se dos dois pontos a seguir: As curvas LR no gráfico 3 são LR = 2 e LR = 0,5, LR = 5 e LR = 0,2, e LR = 10 e LR = 0,1. Os três primeiros múltiplos de "15" são 15, 30 e 45. Usando esta regra, os LRs de 2, 5 e 10 aumentam a probabilidade em cerca de 15%, 30% e 45%, respectivamente. Os LRs de 0,5, 0,2 e 0,1 diminuem a probabilidade em cerca de 15%, 30% e 45%, respectivamente.
Portanto, no paciente hipotético com hipertensão pulmonar, o achado de um regurgitação tricúspide (LR = 10) aumenta a probabilidade de regurgitação tricúspide de 42% para 87% (ou seja, 42% + 45% = 87%).
- Monograma de Fagan
Outra maneira de se obter a probabilide pós-teste a partir de LR e da probabilidade pré-teste é pelo monograma de Fagan, que é facilmente encontrado na internet1.
A coluna da esquerda corresponde a probabilidade pré-teste da doença, a do meio LR e a coluna da direita a probabilidade pós-teste. Para utilizar o monograma, é necessário encontrar a probabilidade pré teste na coluna da esquerda e o LR na coluna do meio, marque os pontos e coloque uma régua conectando os dois pontos e projetando a reta para a coluna da direita (probabilidade pós-teste)5.
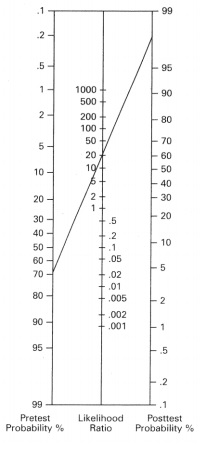
Gráfico 4: Monograma de Fagan
| Vantagens |
1 – Simplicidade
Em um único número, o LR consegue transmitir um achado que argumenta a favor ou contra a doença. Se o LR de um achado for grande, a doença é provável, e se o LR de um achado for próximo de zero, a doença é duvidosa. Esta vantagem permite aos médicos comparar rapidamente diferentes estratégias de diagnóstico e, assim, refinar o julgamento clínico.
2 – Precisão
O uso de LRs para descrever a precisão do diagnóstico é superior ao uso de sensibilidade e especificidade porque os mnemônicos descritos anteriormente, SpPin e SnNout, às vezes são enganosos.
3 - Níveis de descobertas
Outra vantagem dos LRs é que um achado medido em uma escala ordinal (por exemplo, 0, 1, 2, 3) ou em uma escala contínua (por exemplo, pressão arterial) pode ser categorizado em diferentes níveis para determinar o LR para cada nível, aumentando assim a precisão do achado.
Por exemplo, em pacientes com doença pulmonar obstrutiva crônica, os sons respiratórios são tipicamente fracos. Se o médico classificar a intensidade dos sons respiratórios em uma escala de 0 (ausente) a 24 (muito alto), ele pode classificar os sons respiratórios do paciente em um dos quatro grupos: pontuações de 9 ou menos (muito fraco), 10 a 12, 13 a 15, ou maior que 15 (alto)6,7. Cada categoria tem seu próprio LR: pontuações de 9 ou menos aumentam significativamente a probabilidade de doença obstrutiva (LR = 10,2), enquanto escores maiores que 15 diminuem significativamente (LR = 0,1). Escores de 10 a 12 argumentam um pouco para a doença (LR = 3,6), e escores de 13 a 15 não fornecem informações de diagnóstico (LR não é significativamente diferente de 1). Se o médico, em vez disso, tivesse identificado os sons respiratórios como simplesmente "fracos" ou "normais/aumentados”, o achado ainda pode discriminar entre pacientes com e sem doença obstrutiva, mas perde o ponto que tem o poder discriminatório do sinal reside principalmente em pontuações menores que 10 e maiores que 15.
4 – Combinando achados
Os médicos podem combinar os achados, o que é particularmente interessando a achados com LRs entre 0,5 a 2, ou seja achados que sozinhos mudam pouco a probabilidade, mas quando combinados, podem mudar a probabilidade em uma quantidade maior. LRs individuais podem ser combinados, porém, apenas se os achados forem independentes.
| Limitações |
As limitações ocorrem em casos de testes com várias categorias de resultatos ou testes com valores extremos, que geram LR imprecisos8.
Além disso, o principal parâmetro do teste é a prevalência ou a probabilidade prévia da doença. Caso os testes tenham prevalência muito baixa ou muito alta, a chance de um resultado falso-positivo será alta1.
| Conclusão |
O LR tem uma ampla gama de aplicações, incluindo sintomas, exames físicos, exames laboratoriais e procedimentos de imagem.
A utilização de metodologias mais fáceis para achar a probabilide pós-teste, como utilização de monogramas ou gráficos, poderia facilitar o dia a dia dos médicos e aumentar o uso dessa metodologia na prática clínica.